Senin, 13 November 2017
Jumat, 06 Oktober 2017
Rabu, 27 September 2017
kalkulus II
Integral
1. Anti turunan (Integral tak tentu)
Jika kita mengenankan kaos tangan, maka kita dapat melepaskan lagi. Kegiatan kedua dapat menghapuskan kegiatan pertama,mengembalikan kaos tangan padatempat semula. Dapat kita katakan bahwa dua operasi tersebut adalah operasi balikan(invers). Matematika mempunyai banyak pasangan operasi balikan: penambahan dan pengurangan, perkalian dan pembagian, pemangkatan dan penarikan akar, serta penarikan logaritma dan penghitungan logaritma. kita telah mempelajari pendiferensialan (penurunan), balikannya disebut anti pendiferensialan (anti penurunan).
Definisi:
Kita sebut F suatu anti turunan dari f pada selang I jika DF = f pada I, yakni jika F' (x)= f(x) untuk semua x dalam I. (Jika x suatu titik ujung dari I, F' (x) hanya perlu berupa turunan satu sisi
....
1. Anti turunan (Integral tak tentu)
Jika kita mengenankan kaos tangan, maka kita dapat melepaskan lagi. Kegiatan kedua dapat menghapuskan kegiatan pertama,mengembalikan kaos tangan padatempat semula. Dapat kita katakan bahwa dua operasi tersebut adalah operasi balikan(invers). Matematika mempunyai banyak pasangan operasi balikan: penambahan dan pengurangan, perkalian dan pembagian, pemangkatan dan penarikan akar, serta penarikan logaritma dan penghitungan logaritma. kita telah mempelajari pendiferensialan (penurunan), balikannya disebut anti pendiferensialan (anti penurunan).
Definisi:
Kita sebut F suatu anti turunan dari f pada selang I jika DF = f pada I, yakni jika F' (x)= f(x) untuk semua x dalam I. (Jika x suatu titik ujung dari I, F' (x) hanya perlu berupa turunan satu sisi
....
Sabtu, 12 Agustus 2017
Materi Kuliah Matematika Diskrit
diambil dari Hendro Agung S Tempat Berbagi Ilmu
https://hendroagungs.blogspot.co.id/p/my-art.html
Bab 1 Pengantar Matematika Diskrit
Matematika diskrit atau diskret adalah cabang matematika yang membahas segala sesuatu yang bersifat diskrit. Diskrit disini artinya tidak saling berhubungan (lawan dari kontinyu). Objek yang dibahas dalam Matematika Diskrit - seperti bilangan bulat, graf, atau kalimat logika - tidak berubah secara kontinyu, namun memiliki nilai yang tertentu dan terpisah. Beberapa hal yang dibahas dalam matematika ini adalah teori himpunan, teori kombinatorial, permutasi, relasi, fungsi, rekursif, teori graf, dan lain-lain. Matematika diskrit merupakan mata kuliah utama dan dasar untuk bidang ilmu komputer atau informatika.
PPT Preview | Download
Bab 2 Logika
Logika merupakan dasar dari semua penalaran (reasoning). Penalaran didasarkan pada hubungan antara pernyataan (statements).
PPT Preview | Download
Bab 3 Himpunan
Himpunan (set) adalah kumpulan objek-objek yang berbeda. Objek di dalam himpunan disebut elemen, unsur, atau anggota.
PPT Preview | Download
Bab 4 Matriks, Relasi dan Fungsi
Matriks adalah kumpulan bilangan berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks. Dengan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur. Pemanfaatannya misalnya dalam menjelaskan persamaan linier, transformasi koordinat, dan lainnya.
Relasi merupakan hubungan antara dua elemen himpunan.Hubungan ini bersifat abstrak, dan tidak perlu memilik arti apa pun baik secara konkrit maupun secara matematis.
Fungsi digunakan untuk mendefinisikan struktur-struktur diskrit seperti sequense dan string, untuk mendiskripsikan lama waktu yang digunakan dan untuk memecahkan persoalan dengan komputer, atau di dalam ilmu komputer dikenal adanya fungsi rekursif, yaitu fungsi yang memanggil dirinya sendiri.
PPT Preview | Download
Bab 5 Induksi Matematik
Induksi matematis adalah suatu teknik pembuktian penting secara ekstrem dapat digunakan untuk membuktikan pernyataan tegas. Induksi matematis digunakan secara ekstensif untuk membuktikan hasil tentang berbagai objek diskret luas. Misalnya, induksi matematis digunakan untuk membuktikan hasil tentang kompleksitas algoritma, pembetulan tipe program komputer tertentu, teorema tentang graf dan pohon, dan juga suatu range luas dari identitas dan pertidaksamaan.
PPT Preview | Download
diambil dari Hendro Agung S Tempat Berbagi Ilmu
https://hendroagungs.blogspot.co.id/p/my-art.html
Bab 1 Pengantar Matematika Diskrit
Matematika diskrit atau diskret adalah cabang matematika yang membahas segala sesuatu yang bersifat diskrit. Diskrit disini artinya tidak saling berhubungan (lawan dari kontinyu). Objek yang dibahas dalam Matematika Diskrit - seperti bilangan bulat, graf, atau kalimat logika - tidak berubah secara kontinyu, namun memiliki nilai yang tertentu dan terpisah. Beberapa hal yang dibahas dalam matematika ini adalah teori himpunan, teori kombinatorial, permutasi, relasi, fungsi, rekursif, teori graf, dan lain-lain. Matematika diskrit merupakan mata kuliah utama dan dasar untuk bidang ilmu komputer atau informatika.
PPT Preview | Download
Bab 2 Logika
Logika merupakan dasar dari semua penalaran (reasoning). Penalaran didasarkan pada hubungan antara pernyataan (statements).
PPT Preview | Download
Bab 3 Himpunan
Himpunan (set) adalah kumpulan objek-objek yang berbeda. Objek di dalam himpunan disebut elemen, unsur, atau anggota.
PPT Preview | Download
Bab 4 Matriks, Relasi dan Fungsi
Matriks adalah kumpulan bilangan berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks. Dengan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur. Pemanfaatannya misalnya dalam menjelaskan persamaan linier, transformasi koordinat, dan lainnya.
Relasi merupakan hubungan antara dua elemen himpunan.Hubungan ini bersifat abstrak, dan tidak perlu memilik arti apa pun baik secara konkrit maupun secara matematis.
Fungsi digunakan untuk mendefinisikan struktur-struktur diskrit seperti sequense dan string, untuk mendiskripsikan lama waktu yang digunakan dan untuk memecahkan persoalan dengan komputer, atau di dalam ilmu komputer dikenal adanya fungsi rekursif, yaitu fungsi yang memanggil dirinya sendiri.
PPT Preview | Download
Bab 5 Induksi Matematik
Induksi matematis adalah suatu teknik pembuktian penting secara ekstrem dapat digunakan untuk membuktikan pernyataan tegas. Induksi matematis digunakan secara ekstensif untuk membuktikan hasil tentang berbagai objek diskret luas. Misalnya, induksi matematis digunakan untuk membuktikan hasil tentang kompleksitas algoritma, pembetulan tipe program komputer tertentu, teorema tentang graf dan pohon, dan juga suatu range luas dari identitas dan pertidaksamaan.
PPT Preview | Download
Analisis Kompleks
Bilangan Kompleks adalah bilangan yang dinyatakan dalam bentuk a+ib, dimana a dan b adalah bilangan real dan i adalah bagian imajiner dengan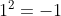 
. Contoh: 2 + i4 adalah bilangan kompleks dengan 2 adalah bagian real dan i4 adalah bagian imajiner.
Dalam sistem bilangan kompleks berada di tingkatan paling atas, seperti yang tampak pada bagan sistem bilangan disamping.
 |
| Bagan Sistem Bilangan |
mata kuliah Analisis Kompleks.
Untuk buku analisis kompleks yang bisa sobat download juga, berikut link nya
Downloaddiambil dari Blog Serba-Serbi Pembelajaran
http://ingrilalan.blogspot.co.id/2014/06/analisis-kompleks.html
JURNAL
1. Jurnal Elektronik Pembelajaran Matematika Vol.2, No.10, hal 1042-1055, Desember 2014
http://www.jurnal.fkip.uns.ac.id/index.php/s2math/article/view/5121
2. Prosiding seminar nasional matematika dan pendidikan matematika
http://ejournal.radenintan.ac.id/index.php/pspm/article/view/1039
3. Seminar Nasional Pendidikan Dasar PGSD Uniflor. Ende, 17 Oktober 2015
1. Jurnal Elektronik Pembelajaran Matematika Vol.2, No.10, hal 1042-1055, Desember 2014
http://www.jurnal.fkip.uns.ac.id/index.php/s2math/article/view/5121
2. Prosiding seminar nasional matematika dan pendidikan matematika
http://ejournal.radenintan.ac.id/index.php/pspm/article/view/1039
3. Seminar Nasional Pendidikan Dasar PGSD Uniflor. Ende, 17 Oktober 2015
Langganan:
Postingan (Atom)
